Criação de um plano de aula utilizando os recursos do Portal do Professor

Por: Vinícius Pinheiro dos Santos e Rafaela Jamile Nascimento Barros

Essa postagem tem o objetivo de demonstrar a criação de um plano de aula qualquer usando apenas os recursos oferecidos pelo Portal do Professor, demonstrando o quão eficiente é esse portal e o quanto ele pode ajudar na construção de aulas dinâmicas e objetivas.

Mas antes de detalhar o referido plano de aula, reservamos um espaço para aqueles que, como nós, são graduandos de cursos de licenciatura, e ainda tem pouco contato com a estrutura de criação de planos de aula e com o Portal do Professor, dando uma pequena definição de ambos.

O que é um plano de aula?

O plano de aula se refere à descrição específica de tudo que o professor executará em sala de aula durante um período determinado, tendo em vista aprimorar a sua prática pedagógica e melhorar o aprendizado dos alunos.

Exemplo de Plano de Aula

Ao elaborá-lo, é importante que preze pela clareza e objetividade, que o atualize periodicamente, que tenha conhecimento dos recursos disponíveis da escola, que saiba sobre as principais características de seus alunos, que aposte em metodologias diversificadas e inovadores e que tenha flexibilidade para lidar com imprevistos no ambiente escolar.

Apesar de não ter um modelo padrão, no plano de aula devem conter: Data e crononograma das atividades, identificação do profissional, tema, objetivos, conteúdo abordado, desenvolvimento do tema (metodologia), recursos didáticos, avaliação e referencial bibliográfico utilizado.

Parece difícil mas não é, inclusive clicando aqui disponibilizamos o plano de aula que construiremos mais adiante no seu formato mais formal.

O Portal do Professor

 

O Portal do Professor

O Portal do Professor, lançado em 2008 em parceria com o Ministério da Ciência e Tecnologia, tem como objetivo apoiar os processos de formação dos professores brasileiros e enriquecer a sua prática pedagógica. Este é um espaço público e pode ser acessado por todos os interessados.

Nesse Portal os professores podem: Produzir e compartilhar sugestões de aulas, acessar informações diversas sobre a prática educacional, acessar e baixar coleção de recursos multimídia, informar-se sobre os cursos e acessar materiais de estudos, interagir e colaborar com outros professores e acessar coleção de links.

 

Recursos Multimídia do Portal

Apesar de só professores poderem se cadastrar para assim compartilharem conteúdo, todas as informações são de acervo público, o que permitiu que pudéssemos criar nosso plano de aula apenas aproveitando de seus ricos recursos.

Plano de Aula: O Tangram como ferramenta para o ensino de área e geometria.

Dadas as definições do que é plano de aula e do Portal do Professor, seguiremos agora com o plano de aula em si. Utilizando o Tangram como ferramenta para o ensino de área e geometria, criamos esse plano de aula mesclando duas propostas de aula dos professores Guilherme Erwin Hartung e Anielle Glória Vaz Coelho e acessando recursos bibliográficos pelo próprio portal. Caso não conheça o Tangram, recomendo que assistam ao vídeo abaixo antes de acessarem o plano de aula.

Lembrando que o referido plano de aula pode ser baixado aqui.

NOTAS:

¹: Orientações de plano de aula sugeridas pela Professora Anielle Glória Vaz Coelho, encontradas no Portal do Professor, no seguinte link:

http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=55733 – acesso em 1º de abril de 2016.

²: Orientações de plano de aula sugeridas pelo Professor Guilherme Erwin Hartung, encontradas no Portal do Professor, no seguinte link:

http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=25696 – acesso em 1º de abril de 2016.

PLANO DE AULA

I. Plano de Aula:

Data: 05 de Abril de 2016

Duração: 04 aulas de 50 minutos cada

Cronograma:

Atividade 1 – 02 aulas de 50 minutos cada

Atividade 2 – 01 aula de 50 minutos

Atividade 3 – 01 aula de 50 minutos

II. Dados de Identificação:

Escola: Escola Pitágoras Proverá (instituição fictícia)

Professores: Vinícius Pinheiro dos Santos e Rafaela Jamile Nascimento Barros

Disciplina: Matemática

Série: 1º Ano do Ensino Médio

Turma: A

Período: 2º Bimestre

III. Tema:

- O Tangram como ferramenta para o ensino de área¹ e geometria².

IV. Objetivos:

Objetivo geral: Trabalhar com o quebra cabeças chinês Tangram, a fim de desenvolver as competências da área 2 da Matriz de Referência de Matemática e suas Tecnologias do ENEM, que é o “H9 - Utilizar conhecimentos geométricos de espaço e forma na seleção de argumentos propostos como solução de problemas do cotidiano” (INEP 2015)¹.

Objetivos específicos:

- Construção e identificação de formas geométricas¹;

- Construção e identificação de diagonais e vértices¹;

- Construção e identificação de ângulos¹;

- Identificar algumas formas geométricas presentes no Tangram²;

- Trabalhar com área e perímetro tendo como "pano de fundo" o Tangram².

V. Conteúdo:

- Grandezas e medidas;

- Espaço e forma;

- Geometria Plana.

VI. Desenvolvimento do tema:

A presente proposta de aula prevê a execução de uma atividade em que o professor montará o Tangram juntamente com os alunos, e a partir daí será realizado um estudo preliminar de área. Nessa proposta, a unidade de medida pré-estabelecida será uma das peças do Tangram.

1ª Atividade: Construção do Tangram¹.

Divida a sala em grupos de 2 (dois) alunos, pois trabalhando em duplas os alunos tendem a se ajudarem mutuamente durante a atividade.

Para iniciar o assunto, o professor pode propor as seguintes questões para os alunos: 

·         O que é um Tangram?

·         Você já brincou com algum? 

Deixe que eles conversem entre si. Após as discussões apresente a história do Tangram e suas peças (Figura 1). 

BREVE HISTÓRIA DO TANGRAM

O Tangram é um antigo quebra-cabeça chinês cuja origem se remonta a uma época desconhecida. O livro mais antigo com figuras de tangram data de 1813. Popular na China com os nomes de "quadrado mágico", "tabela da sabedoria" e "tabela da sagacidade", o tangram é composto por sete peças, as quais são o resultado da partição de um quadrado. As sete peças são: 2 (dois) triângulos grandes, 1(um) triângulo médio, 2 (dois) triângulos pequenos, 1 (um) paralelogramo e 1 (um) quadrado. Com esses simples elementos podem-se formar infinitas figuras.

Fonte: Disponível em <http://migre.me/jf7iK>. Acesso em 02 abril 2016.

Faça a apresentação de cada uma das peças e suas características. Como sugerimos abaixo:

Figura 1: Peças do Tangram¹

Fonte: arquivo da autora¹

Logo após, inicie a construção do Tangram, para isso entregue a cada aluno as instruções a seguir.

COMENTÁRIO: Enfatize a ideia do trabalho coletivo, por isso o estudo, a investigação e as construções deverão ser realizadas juntos com o professor.¹ 

Instruções

Passo 1: Em uma folha de papel A4, recorte um quadrado e nomeie seus vértices ABCD (Figura 2). 

Figura 2 - 1º Passo a ser seguido pelo(a) aluno(a) na Construção do Tangram¹

 

Fonte: arquivo da autora.¹

Alguns questionamentos podem ser feitos nessa primeira etapa.

– Quantos lados tem um quadrado?

Espera-se que os alunos digam quatro lados.

– Quantos ângulos internos temos em um quadrado? Quais são as medidas desses ângulos?

Espera-se que os alunos respondam que o quadrado possui quatro ângulos internos e que cada um desses quatro ângulos mede 90°.

Passo 2: Dobre o quadrado ao meio pelos vértices B e D e destaque com um lápis a linha formada (Figuras 3 e 4)

Figura 3 – 2º Passo da Construção do Tangram¹

Fonte: arquivo da autora¹

 

Figura 4 – Verificação dos ângulos¹

Fonte: arquivo da autora¹

Seguem alguns questionamentos que podem ser feitos nessa etapa da construção.

– Quando dobramos o quadrado ao meio, quais figuras se formaram?

Espera-se que alguns alunos digam que foram formados dois triângulos.

– O que podemos falar sobre a “linha” destacada no quadrado?

Espera-se que os alunos respondam que a linha em destaque é a diagonal do quadrado e que a diagonal de um quadrado o divide em dois triângulos congruentes.

– O que podemos falar sobre os ângulos dos vértices B e D?

Espera-se que os alunos digam que os ângulos dos vértices B e D foram divididos ao meio. 

COMENTÁRIO: Este passo permite explorar o conceito de diagonal de um polígono, que pode ser definido “como o segmento de reta que liga dois vértices não consecutivos”. Com esta informação, os alunos podem concluir, naturalmente, que o quadrado possui duas diagonais. Também, constatar que os ângulos que foram divididos ao meio possuem a mesma medida, pois se sobrepõem e, juntos, formam um ângulo reto. Nesse momento, explorou-se o conceito de bissetriz de um ângulo sem entrar em conceitos formais e pode-se concluiu que a diagonal do quadrado também é bissetriz dos ângulos B e D.¹

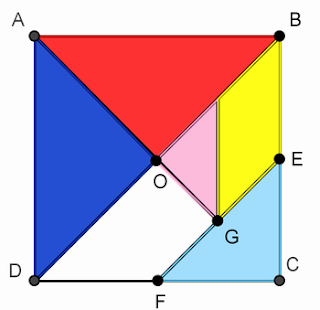
Passo 3: Dobre novamente o quadrado ao meio, mas agora pelos vértices A e C. Faça um vinco apenas na linha que parte de A e encontra a diagonal BC já traçada. Ao abrir o quadrado, marque com o lápis essa linha e nomeie o ponto de encontro das diagonais de O. (Figura 5).

Figura 5 - 3º Passo da Construção do Tangram¹

Fonte: arquivo da autora¹

Figura 6 – Colorindo as peças¹

Fonte: arquivo da autora¹

Oriente os alunos a colorirem o novo triângulo formado AÔD de azul escuro e o novo triângulo formado  AÔB de vermelho. (Figura 6). Levante algumas questões: 

 – O que o segmento OA representa?

Espera-se que os alunos digam que o segmento OA é metade da diagonal do quadrado.

– O que podemos dizer em relação aos segmentos OA e BD?

Espera-se que os alunos respondam que OA é a metade de BD e que são perpendiculares. Caso seja necessário retome com os alunos a ideia de “perpendicular”.

COMENTÁRIO: Até aqui, já foram obtidas duas peças do Tangram. Peças 1 e 2 da Figura 1.¹

Passo 4: Dobre de maneira que o vértice C “encontre” o ponto O. Abra e marque a linha de dobra (Figura 7).

Figura 7 - 4º Passo da Construção do Tangram¹

Fonte: arquivo da autora¹

Figura 8 – Colorindo novas peças¹

 Fonte: arquivo da autora¹

 ­­­­­­

Solicite aos alunos para nomear os vértices E e F, e colorir de azul claro o triângulo FCE (Figura 8). Questione:

– O que podemos verificar sobre as medidas dos segmentos DF e FC? E sobre as medidas dos segmentos BE e EC? Como os pontos E e F podem ser chamados?

Espera-se que os alunos observem que as medidas dos segmentos DF  e FC são iguais, bem como as medidas dos segmentos BE e EC. A partir desse procedimento, também se identificam os pontos E e F como os pontos médios dos lados BC e CD, respectivamente. Além de concluir que as medidas de DF,  FG,  BE  e EC são iguais.

COMENTÁRIO: Neste passo, obteve-se a peça 3 (Figura 1) do Tangram¹

Passo 5: Dobre novamente a diagonal AC  e faça um vinco até o encontro do segmento EF. Nomeie o ponto de intersecção G. Marque essa linha de dobra. Dobre, então, de modo que o ponto E toque o ponto O. Vire a dobra entre o ponto G e a diagonal BD. Abra e marque esse segmento (Figura 9).

Figura 9 - 5º Passo da Construção do Tangram¹

Fonte: arquivo da autora¹

Figura 10 – Colorindo as peças do passo 5¹

Fonte: arquivo da autora¹

       

Solicite que coloram o triângulo que tem os pontos O e G como vértices de rosa claro e o paralelogramo formado de amarelo. (Figura 10).

Nesse passo, pode-se explorar as propriedades dos lados, ângulos e diagonais do paralelogramo.  A seguir seguem algumas sugestões: 

– Todo paralelogramo possui quantos vértices? Quantos lados? Quantos ângulos internos? Quantos ângulos externos? Quantas diagonais?

Espera-se que os lados respondam que todo paralelogramo possui quatro vértices, assim como quatro lados, quatro ângulos internos, quatro ângulos externos e duas diagonais.

– O que podemos dizer sobre os lados e os ângulos de um paralelogramo?

Espera-se que os alunos digam que os lados opostos de um paralelogramo são iguais e paralelos e, em consequência, tem ângulos opostos congruentes.

COMENTÁRIO: Com este passo, foram obtidas as peças 4 e 5 (Figura 1) do Tangram¹.

Passo 6: Para obter as peças que faltam para completar o Tangram, dobre de maneira que o vértice D toque o ponto O. Vinque essa dobra do ponto F até a diagonal BD  (Figura 11).

Figura 11 - 6º Passo da Construção do Tangram¹

Fonte: arquivo da autora¹

Figura 12 – Colorindo as últimas peças¹ 

 Fonte: arquivo da autora¹

Questione os alunos sobre quais peças foram formadas nesse passo e oriente-os a colorir o triângulo de verde e o quadrado de laranja. (Figura 12).

COMENTÁRIO: Assim, com as peças 6 e 7 (Figura 1) o Tangram está completo. Nesta última etapa, os alunos podem classificar o triângulo obtido e verificar que o quadrilátero formado é um quadrado. Isso ocorreu por meio da comparação da medida de seus lados e ângulos com dobras nas duas diagonais do quadrilátero.¹

Sugira que os alunos sinalizem com um símbolos como (*), (#), (%), (+) e (●) as peças obtidas, da seguinte forma: símbolos iguais para figuras congruentes e símbolos diferentes para não congruentes. (Figura 13).

Figura 13 – Selecionando peças congruentes¹

Fonte: arquivo da autora¹

COMENTÁRIO: Caso seja necessário retome com os alunos a ideia de congruência, em que consideramos a semelhança (por sobreposição) ou equivalência de características das peças.¹

2ª Atividade: Gincana de construção de figuras geométricas². 

Esta atividade está planejada para ser realizada em grupos de quatro ou cinco alunos. O professor precisará de um conjunto de tangram para cada grupo.

Sugiro que essa atividade seja uma gincana, onde o professor lançará "tarefas relâmpago" (Façam um triângulo retângulo isósceles com 4 peças, por exemplo). O grupo que conseguir cumprir a tarefa primeiro pontua na gincana.

Fonte: arquivo do autor²

 

Vá aumentando a complexidade gradativamente.

Fonte: arquivo do autor²

Ainda com quadrados é possível lançar esses desafios:

1) Monte um quadrado com quatro peças usando apenas triângulos.

2) Monte agora outro quadrado com a mesma área do quadrado anterior.

Inclua os retângulos.

Fonte: arquivo do autor²

Trabalhe com os dois trapézios, o isósceles e o retângulo.

 

Fonte: arquivo do autor²

Ainda em quadriláteros, aborde os paralelogramos.

Fonte: arquivo do autor²

Os Pentágonos:

  

Fonte: arquivo do autor²

Hexágonos:

Fonte: arquivo do autor²

E até mesmo heptágonos:

Fonte: arquivo do autor²

3ª Atividade: Questões avançadas de Geometria com o uso do Tangram.²

Como terceira atividade, deixo questionamentos mais complexos e podem ser feitos de forma individual. Veja:

Será que as peças vão se encontrar perfeitamente de modo que a base maior do trapézio (composto do paralelogramo e do triângulo médio) coincida com a hipotenusa do triângulo maior? Demonstre. Peça para os alunos comentarem as estratégias usadas por eles para desenvolver a solução do problema.

Veja a solução sugerida abaixo:

Fonte: arquivo do autor²

Outro questionamento para ser proposto: Se considerarmos o lado do quadrado retirado como 1 cm, qual é a área do Tangram que restou?

Fonte: arquivo do autor²

Novamente discuta com os alunos estratégias para responder o problema.

Veja uma sugestão para a solução do problema:

Fonte: arquivo do autor²

Mais um problema: Que ângulo obtuso é esse? Existem diversas maneiras de resolver esses problemas. Discuta com seus alunos outras formas de resolvê-los.

Fonte: arquivo do autor²

VII. Recursos didáticos:

 - Quadro

- Giz

- Folha de papel A4 branca.

- Tesoura

- Lápis

- Lápis para colorir

VIII. Avaliação:

Recomenda-se, como processo de avaliação, que o professor observe o interesse, a motivação e o envolvimento dos alunos na realização da atividade sugerida e na participação durante as discussões do grupo, pois, conforme apontam os PCN, a participação em grupos representa “uma conquista cognitiva, emocional, moral e social para a criança e um estímulo para o desenvolvimento do seu raciocínio lógico” (BRASIL, 1997, p. 36).

Pode-se ainda, adotar como critério avaliativo formal o registro individual dos alunos quanto suas respostas nas diferentes etapas da atividade¹.

XIX. Bibliografia:

BRASIL. Ministério da Educação. Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira – INEP. Edital Nº 6, de 15 de maio de 2015, Exame Nacional do Ensino Médio. Brasília: INEP, Brasília, 2015.

______. Ministério da Educação. Secretaria de Ensino Fundamental. Referenciais para a formação de professores. Brasília: MEC/SEF, Brasília, 1997.

______. Secretaria de Educação Fundamental. Parâmetros curriculares nacionais: Matemática. Brasília: MEC/SEF, Brasília, 1998.